Contoh Soal Dinamika Rotasi dan Penyelesaiannya – Dalam pembahasan mengenai Hukum Newton, telah Anda ketahui bahwa dalam resultan gaya yang bekerja pada suatu benda akan mengakibatkan perubahan percepatan pada benda tersebut. Resultan gaya tersebut akan menyebabkan terjadinya gerak bergeser suatu benda (translasi). Selain gerak translasi, dikenal pula gerak rotasi (berputar). Apakah yang dapat menyebabkan terjadinya gerak rotasi?
Gerak rotasi pun disebabkan oleh sejumlah gaya yang bekerja pada suatu benda. Bagaimanakah gay aini dapat menyebabkan terjadinya gerak rotasi, perhatikan gambar berikut:
Dari gambar diatas, 3 buah gaya bekerja pada sebuat batang/tongkat yang memiliki pusat putaran di titik O. F1 memiliki jarak sebesar r1 terhadap titik O, F2 memiliki jarak sebesar r2 terhadap titik O dan F3 bekerja pada tongkat namun tidak memiliki jarak terhadap titik O.
Contoh Soal Dinamika Rotasi dan Penyelesaiannya
Momen inersia untuk system partikel
Contoh Soal:
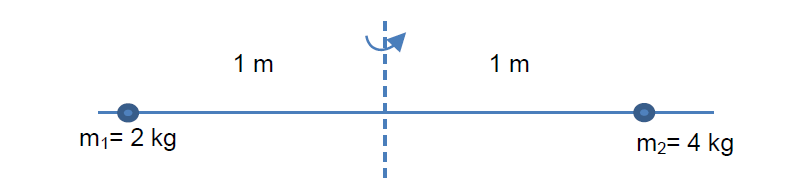
Dua buah benda bermassa 2 kg dan 4 kg terpisah sejauh 2 m yang terpasang pada suatu tongkat ringan (massa tongkat diabaikan). Hitunglah momen inersia dari sistem jika:
(a) sumbu putar terletak tepat di tengah-tengah antara kedua benda
(b) sumbu putar terletak di sejauh 1 m di sebelah kanan benda bermassa 4 kg.
Jawab:
Perhatikan gambar berikut:
Ada dua benda pada sistem, sehingga gunakan Persamaan inersia untuk mengerjakan:
Perhatikan gambar berikut:
Nilai inersia system tersebut diatas adalah:
Momen Inersia untuk benda Kontinu
Contoh Soal
Cari momen inersia dari tongkat sepanjang L dan bermassa m yang terdistribusi merata dengan sumbu putar yang terletak pada salah satu ujung tongkat dan tegak lurus dengan tongkat!
Jawab:
Sebelumnya bila kita asumsikan bahwa tongkat adalah tipis sekali, sehingga dapat dianggap sebagai benda satu dimensi.
Apabila,
maka akan diperoleh persamaan
Sehingga bila dimasukkan kedalam persamaan integral diatas akan menjadi:
Karena jarak elemen massa dm ke pusat putaran adalah x, maka r dapat diganti menjadi x. Akibatnya persamaan diatas menjadi:
Teorema Sumbu Sejajar
Contoh Soal:
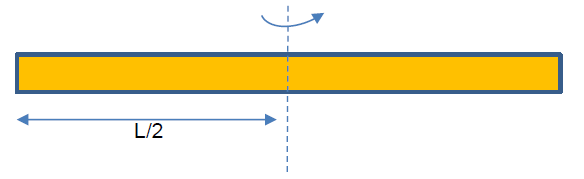
Hitunglah momen inersia dari tongkat tipis dengan sumbu putar yang melewati pusat massanya!
Jawab :
Kita gunakan informasi momen inersia tongkat tipis yang diputar pada ujung tongkat seperti pada contoh 3 yaitu:
Letak pusat massa dari tongkat tipis adalah di tengah-tengah tongkat seperti ditunjukkan pada gambar berikut.
Sehingga diperoleh persamaan:
Berikut ini diberikan table persamaan momen inersia untuk beberapa benda.
